Rumus Mencari Keliling Lingkaran Yang Diarsir

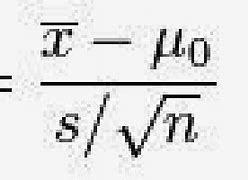
Sifat-sifat Lingkaran

Berikut ini sifat-sifat dari lingkaran:

Dikutip melalui buku berjudul Geometri Datar karya Fuat (2020), keliling lingkaran adalah ukuran panjang lingkaran yang dinyatakan dengan satuan panjang garis. Sederhananya, keliling merupakan jarak 1 putaran dari suatu titik lingkaran ke titik itu sendiri.

Di bawah ini adalah rumus keliling lingkaran, dikutip melalui buku berjudul Mandiri Belajar Ulangan Tematik karya Desi Damayanti, dkk.

Contoh Soal Keliling Lingkaran Jika yang Diketahui Diameternya

1. Diketahui sebuah lingkaran memiliki diameter 42 cm. Tentukan berapa keliling lingkaran tersebut!Pembahasan:Diketahui:d = 42 cmπ = 22/7

K = π x dK = 22/7 x 42 cmK = 132 cm

Jadi, keliling dari lingkaran dengan diameter 42 cm adalah 132 cm.

2. Hitunglah berapa keliling lingkaran yang memiliki diameter 28 cm!Pembahasan:Diketahui:d = 28 cmπ = 3,14

K = π x d K = 3,14 x 28 cmK = 87,92 cm

Jadi, keliling dari lingkaran dengan diameter 28 cm adalah 87,92 cm.

Contoh Soal Keliling Lingkaran 1

Keliling lingkaran dengan jari-jari 14 cm adalah...

a. 22 cmb. 44 cmc. 88 cmd. 110 cm

Jari-jari = r = 14 cmKeliling lingkaran = 2πrK = 2 x (22/7) x 14 cmK = 88 cm

Maka jawaban yang benar adalah C.

Rumus Keliling Lingkaran

Keliling lingkaran dapat dihitung dengan mengetahui nilai Pi (π) dan jari-jari atau radius lingkaran (r) atau diameter lingkaran (d). Rumus keliling lingkaran adalah K = 2πr atau K = πd. K merupakan lambang keliling lingkaran. Sedangkan nilai π yaitu 22/7 atau 3,14.

Jika diketahui diameter, maka rumus keliling lingkaran adalah K = πd

Jika diketahui jari-jari, maka rumus keliling lingkaran adalah K = 2πr

Apa yang Dimaksud dengan “Lingkaran”?

Secara singkat, lingkaran adalah salah satu bangun datar. Jenis bangun datar yang mirip bentuk ban sepeda ini memiliki berbagai rumus yang nggak terlepas dari bagian ilmu Matematika. Kita akan mengetahui serba-serbi rumus lingkaran yang akan kita ulas kali ini.

Namun sebelum itu, kenalan dulu yuk, dengan identitas dari lingkaran.

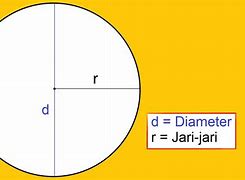
Lingkaran adalah himpunan semua titik di bidang yang berjarak sama dari suatu titik tetap. Titik tetap ini yang kemudian disebut sebagai pusat lingkaran. Sedangkan, jarak dari pusat ke setiap titik disebut dengan jari-jari.

Biar lebih tergambar, Skollamate bisa lanjut baca bagian di bawah ini untuk tahu detail tentang unsur-unsur lingkaran, ya!

Contoh Soal Keliling Lingkaran Jika yang Diketahui Luasnya

1. Diketahui sebuah lingkaran memiliki luas 314 cm². Berapa kira-kira keliling dari lingkaran tersebut?Pembahasan:Diketahui:L = 314 cm²π = 3,14

Untuk menentukan keliling, dicari terlebih dahulu jari-jarinya dengan menggunakan rumus luas lingkaran:L = π x r²314 = 3,14 x r²r² = 314/3,14r² = 100r = 10

Setelah diketahui jari-jarinya 10, selanjutnya hitung kelilingnya:K = 2 x π x rK = 2 x 3,14 x 10K = 2 x 31,4K = 62,8 cm

Jadi, keliling dari lingkaran yang mempunyai luas 314 cm² adalah 62,8 cm.

2. Diketahui sebuah lingkaran mempunyai luas 1256 cm². Hitunglah berapa keliling lingkaran tersebut!Pembahasan:Diketahui:L = 1256 cm²π = 3,14

Untuk menentukan keliling, dicari terlebih dahulu jari-jarinya dengan menggunakan rumus luas lingkaran:L = π x r²1256 = 3,14 x r²r² = 1256/3,14r² = 400r = 20

Setelah diketahui jari-jarinya 10, selanjutnya hitung kelilingnya:K = 2 x π x rK = 2 x 3,14 x 20K = 2 x 62,8K = 125,6 cm

Jadi, keliling dari lingkaran yang mempunyai luas 1256 cm² adalah 125,6 cm.

Demikian yang dapat detikEdu sampaikan mengenai rumus keliling lingkaran beserta dengan contoh soalnya. Semoga bermanfaat!

Artikel ini disusun bersama

. Grace Imson adalah guru matematika dengan 40 tahun pengalaman mengajar. Grace saat ini adalah pengajar matematika di City College of San Francisco dan sebelumnya bekerja di Math Department di Saint Louis University. Dia mengajar matematika di sekolah dasar, sekolah menengah, dan perguruan tinggi. Grace memiliki gelar MA dalam Pendidikan, dengan spesialisasi Administrasi dan Pengawasan, dari Saint Louis University. Artikel ini telah dilihat 596.204 kali.

Halaman ini telah diakses sebanyak 596.204 kali.

Contoh Soal dan Pembahasan

Setelah tahu rumus-rumus lingkaran, inilah saatnya mengaplikasikan rumus tersebut ke dalam soal. Coba jawab soal tanpa scroll jawabannya, ya! Yuk, bersiap coret-coret dan simak contoh soalnya di bawah ini!

Sebuah lingkaran memiliki jari-jari 7 cm. Hitung keliling dan luas lingkaran tersebut. Gunakan π = 22/7.

Maka, keliling lingkaran tersebut adalah 44 cm dan luasnya 154 cm².

Sebuah lingkaran memiliki diameter 14 cm. Hitung keliling dan luas lingkaran tersebut. Gunakan π = 3,14.

L = 153,86 cm² atau 154 cm²

Maka, keliling lingkaran tersebut adalah 43,96 cm dan luas lingkarannya adalah 152,86 cm².

Sebuah lingkaran memiliki keliling 31,4 cm. Hitung jari-jari dan luas lingkaran tersebut. Gunakan π = 3,14.

Maka, jari-jari lingkaran tersebut adalah 5 cm dan luas lingkarannya adalah 78,5 cm².

Itu dia seluk-beluk perihal bangun datar bernama lingkaran, yang wujudnya kerap mengingatkan pada bola, uang koin, tutup botol, dan masih banyak benda-benda familiar di sekitar kita.

Nah, buat Skollamate yang ingin memperkaya ilmu Matematika dengan cara yang menyenangkan, kamu bisa menyimak pembahasannya lebih lanjut di aplikasi Skolla. Nggak cuma soal lingkaran dan matematika, tapi ada banyak materi lainnya yang bisa kamu pelajari di sana. Cek aplikasi Skolla untuk mulai belajar!

Rumus keliling lingkaran digunakan untuk menghitung panjang antara titik A di garis keliling lingkaran ke titik itu kembali. Begini cara menghitungnya dengan rumus keliling lingkaran.

Dikutip dari Pasti Bisa Matematika untuk SD/Mi Kelas VI oleh Tim Tunas Karya Guru, kamu perlu mengenal unsur lingkaran untuk menghitung keliling lingkaran. Unsur lingkaran yang digunakan dalam rumus keliling lingkaran yaitu jari-jari atau radius (r) dan diameter atau garis tengah (d).

Unsur lingkaran di antaranya:

SCROLL TO CONTINUE WITH CONTENT

- Titik pusat (titik O), yaitu titik yang terletak di tengah-tengah lingkaran- Jari-jari atau radius (r), yaitu garis dari titik pusat lingkaran ke lengkungan lingkaran- Diameter (garis tengah), yaitu garis lurus yang menghubungkan dua titik pada lengkungan lingkaran dan melalui titik pusat- Busur, yaitu garis lengkung yang terletak pada lengkungan lingkaran dan menghubungkan dua titik sebarang pada lengkungan tersebut- Tali busur, yaitu garis lurus dalam lingkaran yang menghubungkan dua titik pada lengkungan lingkaran- Juring, yaitu luas daerah dalam lingkaran yang dibatasi dua buah jari-jari lingkaran dan sebuah busur yang diapit kedua jari-jari lingkaran tersebut

Contoh soal keliling lingkaran dengan diameter

Danial sedang berenang di kolam berbentuk lingkaran. Sebelum mengitarinya, ia terlebih dahulu ingin mengetahui keliling lingkaran. Apabila diketahui diameternya sepanjang 20 meter, maka berapa kelilingnya?

Yang diketahui dari soal adalah diameter. Maka, menggunakan rumus Keliling Lingkaran = π x d. Kedua, karena panjang diameter bukanlah kelipatan tujuh, maka phi yang digunakan adalah 3,14. Adapun tahapan menghitungnya yakni:

Nah, panjang keliling kolam yang hendak diputari Danial adalah 62,8 meter.

Contoh Soal Perhitungan Keliling Lingkaran

Melansir smpn3payakumbuh.sch.id, berikut contoh soal dan pembahasan keliling lingkaran:

Hitunglah keliling lingkaran yang mempunyai diameter 15 cm dengan π = 3,14.

Keliling = πd = 3,14 x 15 cm = 47,1 cm.

Hitunglah diameter lingkaran yang mempunyai keliling 25,12 cm dan π = 3,14.

Jadi, diameter lingkaran tersebut adalah 8 cm.

Tentukan keliling lingkaran yang berdiameter 21 cm dan π = 22/7.

Keliling = πd = 22/7 x 21 cm = 22 x 3 cm = 66 cm.

Tentukan keliling lingkaran yang berdiameter 35 cm dan π = 22/7.

Keliling = πd = 22/7 x 35 cm = 22 x 5 cm = 110 cm.

Tentukan keliling lingkaran yang berdiameter 49 cm dan π = 22/7.

Keliling = πd = 22/7 x 49 cm = 22 x 7 cm = 154 cm.

Tentukan keliling lingkaran yang berdiameter 38,5 cm dan π = 22/7/

Keliling = πd = 22/7 x 38,5 cm = 22 x 5,5 cm = 121 cm.

Tentukan keliling lingkaran yang panjang jari-jarinya 10 cm dan π = 3,14.

Keliling = 2πr = 2 x 3,14 x 10 cm = 62,8 cm.

Tentukan keliling lingkaran yang panjang jari-jarinya 15 cm dan π = 3,14.

Keliling = 2πr = 2 x 3,14 x 15 cm = 94,2 cm.

Tentukan keliling lingkaran yang panjang jari-jarinya 36 cm dan π = 3,14.

Keliling = 2πr = 2 x 3,14 x 36 cm = 226,08 cm.

Tentukan keliling lingkaran yang panjang jari-jarinya 15,5 cm dan π = 3,14.

Keliling = 2πr = 2 x 3,14 x 15,5 cm = 97,34 cm.

Diameter mata uang koin lima ratus rupiah adalah 15 mm. Hitunglah kelilingnya.

Keliling = 2πr = 2 x 3,14 x 15 mm = 94,2 mm.

Diameter sebuah roda mobil adalah 42 cm. Hitunglah keliling roda tersebut.

Keliling = πd = 22/7 x 42 cm = 22 x 6 cm = 132 cm.

Skollamate, ketika pertama kali mendengar lingkaran, apa yang ada di pikiranmu? Hmm… Ban sepeda, kancing, jam dinding, atau pizza? Betul! Pasti kamu bisa menyebutkan banyak benda berbentuk lingkaran.

Tahukah kamu kalau benda yang kamu sebutkan tadi adalah gerbang dari sebuah konsep ilmu Matematika?

Ya! Tanpa kamu sadari, dulu kamu mengenal lingkaran hanya sebagai jenis “bentuk”. Tapi sekarang, kamu akan mengenal lingkaran lebih jauh lagi sebagai salah satu dari konsep Matematika, yaitu “bangun datar”. Menarik, kan?

Nggak sebatas bentuknya melingkar, kamu akan lebih tau serba-serbi tentang lingkaran. Kamu juga bakal ketemu rumus lingkaran yang nggak cuma ada satu. Penasaran mau pelajarin lebih lanjut? Yuk, baca di artikel ini!